
Mind hämmastab poliitikute emotsionaalne käsitlus koroonaviirusega seonduvate piirangute rakendamisest ning ratsionaalsete valikute avaldamise puudulikkus. Tegemist on haritud inimestele kooliajast selge matemaatilise optimeerimisülesande lahendamisega.
Toome näite. Kõigepealt kehtestame optimeerimisüles eeldused.
Esimene eeldus – on seos koroonaviiruse juhtude ja majandustegevuse aktiivsuse vahel. Teiseks – piirangute leevendudes koroonaviirusesse haigestumise arv tõuseb. Kolmas eeldus – toimivat vaktsiini pole ja selle valmimisega ei saa arvestada.
Räägime eeldused lähemalt lahti. Kõigepealt – piirangud vähendavad haigestumisriski, kuid toovad kaasa majandustegevuse aktiivsuse languse. Väheneb ettevõtete võimekus maksta makse riigile ja töötasu töötajatele. Töökohtade vähesus võib kaasa tuua teatud gruppide ettenägematu sotsiaalse käitumise, suurendades koroonaviiruse levimise riski.
Järgmiseks – piirangute leevendamine tõstab haigestumismäära, s.o. meditsiinikulusid ja tõstab küll ettevõtete majanduslikku aktiivsust, kuid võib kaasa tuua ka ettenägematud kulud mingit liiki tarbimise sulgumise tõttu (näiteks hirm osaleda üritustel, naaberriikide reageeringud).
Haigestumismäär ning surmade arv sõltub kultuurilisest kontekstist (käitumisharjumused, sotsiaalne kontroll ja hinnang üksteise käitumisele) ning demograafilisest situatsioonist (sotsiaalsete gruppide tervislikust seisundist) Tähistame piirangute ranguse tähisega R, juhtude arvu J, majandusliku tegevuse taseme M, majandusliku aktiivsuse väljundiga seotud kahjud V. Kehtestame optimeerimisülesande – leida tasakaal piirangute ranguse ja majandusliku aktiivsuse taotlemise vahel.
Otsustusvälja mudel oleks vastavalt allpool toodud joonisele.
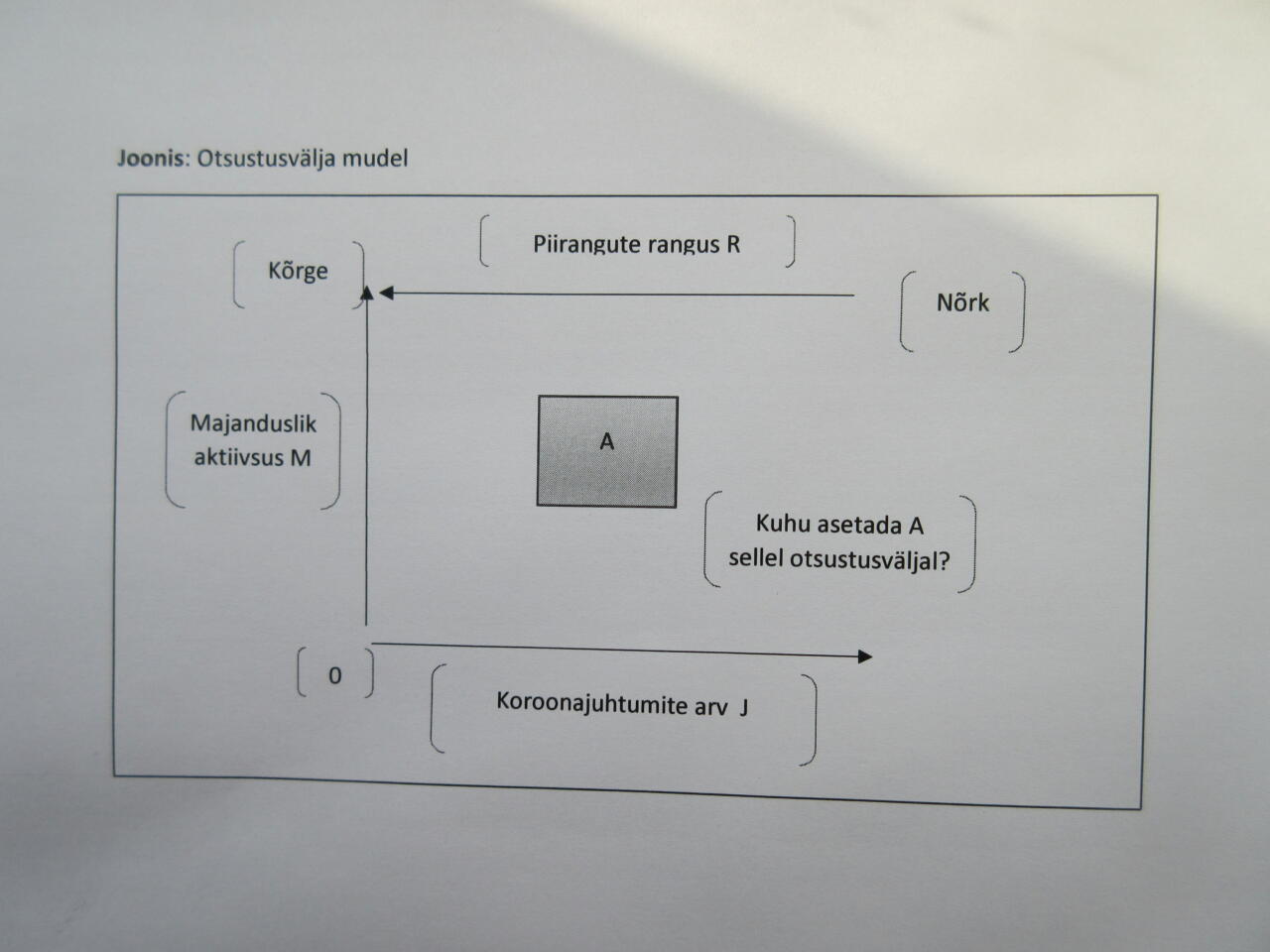
Seega optimeerimisülesande lahendamine peaks vastama, kuhu asetada A ning mis võtta valikute aluseks. Kas selleks on: ainult majanduslikud kaalutlused (kulud ja tulud), sotsiaalsed ja majanduslikud (nende kulude ja tulude arvutamine on väljaspool antud arvamuse teemat, aga teoreetiliselt võimalikud) või mingid väärtuspõhised (näiteks hinnang inimelu väärtusele). Seega me hakka siin arutlema kompromisskõvera täpse olemuse üle, jutt läheks üsna pikaks.
Surmajuhtumite arv s on seoses pandeemia leviku määraga – mida rohkem on pandeemia levinud, seda tõenäosem on surmajuhtumite esinemine ning seda rohkem tuleb piirata majandustegevust ning vähendada majanduslikku aktiivsust.
Surmajuhtumeid kajastame valemis: s = f(J), kus f′ > 0
Surmajuhtumeid pole võimalik täiesti välistada, kuid eesmärk on neid maksimaalselt vähendada. Edasi tuleks arvutada majandusliku aktiivsuse määr igal võimalikul koroonaviiruse leviku tasemel: M = g(J)
Majanduslikud kahjud oleksid: V = Mo − g(J) , kus Mo näitaks kahjude ulatust koroonaviiruse puudumisel (koroonaviirusest tulenevad kahjud puuduvad, samuti piirangute rangus on 0.
Sotsiaalne ootus on võimalikult madal koroonahaigestumiste arv ja võimalikult kõrge majanduslik aktiivsus. Ebareaalsed on ootused, et piirangud on nõrgad, koroonajuhtumiste arv väike ja majanduslik aktiivsus kõrge. Pigem on tõenäoline kombinatsioon, kus piirangud on suhteliselt ranged, koroonaviiruse levik on mõõdukas ning majanduslik aktiivsus samuti mõõdukas.
Eelistuste kombinatsiooni arvutamiseks võib vaadata A. Bergsoni 1938 aasta tööd. Poliitiline surve piirangute ranguse lõdvendamiseks viib haigusjuhtumite arvu tõusule.
Eespool öeldu põhjal mõningad soovitused. Esiteks – kuna tegemist on matemaatikaga, siis võiks mõned tulevikuarengute alternatiivid välja arvutada. See oleks ka vastuseks opositsiooni nõudele esitada pandeemiast väljumise plaanid.
Teiseks – lähenevate valimiste valguses võiks rahvaesindajate kandidaatidelt nõuda ka mõningaid matemaatilisi võimeid ning oskust oma ettepanekuid matemaatilises mudelis esitleda. Kuna koroonaviirusest tulenevaid otsuseid tuleb teha ka kohalikul tasandil, siis ilmselt oleks võimalik matemaatiliste mudelite alusel leida üsna suurt üksmeelt saavutavaid lahendeid.
Alver Aria, lihtsalt kõrvalseisja